Voici un texte intéressant à plus d’un titre. Le groupe Ouest de Méthode naturelle de mathématiques l’a beaucoup apprécié. Grâce à lui, nous allons pouvoir amorcer une réflexion approfondie sur nos pratiques ; et confronter, par exemple, l’option « recherches libres » et l’option « méthode naturelle » qui a pour base la création-expression ou, si l’on préfère, le texte libre mathématique.
« Le but d’une discussion n‘étant ni l’accord, ni la victoire mais le fait de faire progresser les vues de chacun. »
La méthode naturelle
Pour bien situer les choses, rappelons rapidement que notre méthode naturelle (MN) se caractérise essentiellement par l’expression-création quasi-journalière. Puis des productions de chacun sont présentées régulièrement aux autres pour observations, commentaires et discussion critique par la petite « communauté scientifique » que constitue le demi-groupe.
Évidemment, les créations qui sont autant d’idées, d’hypothèses, de théories personnelles sont chargées d’affectivité. Cependant il se construit inter-subjectivement un savoir réel. Il y a un surgissement des problèmes, une critique instantanée, une remise en cause incessante, une surprise de la création des autres, un agrandissement du regard, une défense soutenue de sa propre théorie ; comme s’il fallait une maturation pour découvrir et accepter ses erreurs. Avec, au passage, pour le maître, la découverte de personnalités à dominantes d’invention, d’imagination débridée, de critique ergoteuse ou réfléchie, d’application automatique à la réalité, de don de l’erreur féconde.
Le désir
Pour essayer de mieux cerner la conception de Jany Gibert et de tous ceux qui pratiquent les recherches-libres, je reprends son texte. Il commence avec raison par parler du désir de l’enfant. Là, nous sommes d’accord, c’est un point central. Pour nous, c’est cela même qui fonde notre MN.
La preuve, c’est que lorsque nous cessons de la pratiquer, il y a des réclamations. Il y a un plaisir certain qu’il faut peut-être analyser. Hâtons-nous de dire qu’il ne s’agit pas « d’apprendre en riant ». Ce serait trop nier la réalité du travail et de l’effort. Mais existent certainement le plaisir d’être accepté, considéré, reconnu, le plaisir de provoquer en dissimulant des structures, de collaborer, de découvrir, d’offrir de nouvelles pistes, de s’investir profondément, d’acquérir un savoir réel, immédiatement utilisable, de permettre de déboucher sur un problème encore plus intéressant parce que plus large, plus englobant, etc.
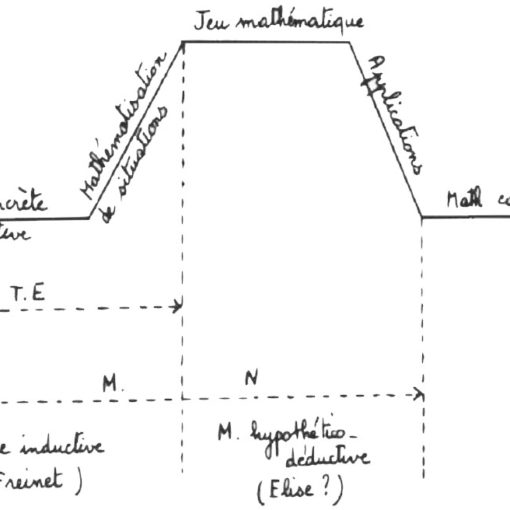
Et la mathématique est aussi un langage. Et la MN une occasion de langages. Ils ont des fonctions de description, d’appel, d’argumentation. Mais aussi de poésie, d’expression et même d’équilibration psychologique. Aussi, quand ils sont vraiment libres de leurs textes libres, les enfants s’en donnent à cœur joie. Rien à craindre à ce sujet :
« La conception hypothético-déductive et la description de la méthode constituent une invitation à multiplier les hypothèses et même à proposer les conjectures les plus audacieuses possibles. Nous avons besoin de théories hautement improbables si nous voulons apprendre quelque chose. »
Mais il ne s’agit pas de créer gratuitement.
Les théories sont des filets destinés à capturer ce que nous appelons « le monde », à le rendre rationnel, à l’expliquer, à le maîtriser. Mais ne nous attardons pas sur ce désir de l’enfant qui est peut-être plus fondamental encore que nous ne le pressentons.
« Tout organisme naît avec des attentes et des dispositions innées. »
Nous avons d’abord à pratiquer abondamment la MN.
L’erreur
Là aussi accord avec Jany. D’autant plus qu’il se réfère, lui aussi, à Bachelard. Mais celui-ci pense que si l’erreur n’est pas un mal, elle n’en est pas moins déplorable. Ce n’est pas l’avis de Karl Popper qui pense qu’elle est indispensable.
« L’erreur n’est plus ce que la raison doit fuir mais ce qu‘elle doit provoquer. La science n‘est donc pas le lieu de la sécurité, mais de l’insécurité. »
Anti-inductivisme
Mais ces deux philosophes se rejoignent sur un point capital pour nous. C’est la théorie qui est première. Il n’y a pas d’observation sans théorie préalable.
« Une idée anticipée ou une hypothèse est donc le point de départ nécessaire de tout raisonnement expérimental ; sans cela... on ne pourrait qu’entasser des observations stériles. » (Claude Bernard)
Les faits ne peuvent être observés que si l’esprit fonctionne comme un faisceau lumineux, éclairant le monde de façon sélective. C’est pour cela que Popper est contre l’induction. Induire, c’est accumuler des informations, constater des répétitions, avoir l’idée de lois qui sont vérifiées par les observations en leur faveur et qui finissent par être définitivement établies et certaines. En s’ajoutant les unes aux autres, les lois atteignent une universalité de plus en plus grande, en un processus indéfini de généralisation.
À la suite de Freinet, du moins me semble-t-il, beaucoup de ses disciples partagent cette conception de la connaissance. Mais – peut-être en accord avec Élise, sa femme – on peut concevoir une autre démarche.
« Dans la démarche inductive, tout l’effort de la connaissance est un effort de vérification et de justification des théories, et cet effort peut, lui, être couronné de succès. On part donc de la théorie et on ne se sert de l’observation que pour tenter de l’infirmer. »
Cela change considérablement les choses. Et nous avons pu le vérifier dans nos classes. Il y a production abondante de théories mais toujours tentatives de vérification expérimentale pour en contester la solidité. Celles qui résistent constituent – provisoirement – le savoir. C’est ainsi que fonctionne la science. Cependant :
« La science ne se conçoit pas sans un ensemble d’institutions permettant la communication des idées – absence de censure, organisation des moyens d’échanges des idées, par exemple – les conditions de possibilité de la méthode critique sont sociales et non individuelles. »
Mais c’est précisément ce que nous apporte Freinet : cette conception du rôle du groupe – alors qu’Élise semblait se fonder davantage sur l’individuel. Et il nous a apporté aussi le texte libre. Maintenant, on peut rêver de donner une cohérence plus poussée à notre pédagogie en nous engageant dans les voies du travail libre scientifique, juridique, corporel, musical, artistique... Mais c’est un autre sujet.
L’anxiété
L’anxiété est très grande quand il s’agit d’une question extérieure posée par le maître, ou le livre, ou l’ordinateur... ou le formateur sadique qui jouit de son pouvoir. Comment leur échapper ? Mais la situation est différente quand il s’agit d’une question issue de la classe. Ce sont des pairs (et non des pères) qui la posent et qui participent souvent à la recherche de la solution, car
« L’homme invente des théories et des idées... mais une fois qu‘il les a créées, il ne peut plus les maîtriser, il les rencontre dans leur opacité, il se heurte à elles. »
« Les maths sont l’exemple parfait d’une création de l’homme qui échappe à son créateur. L’homme est dans l’obligation d’explorer patiemment ce monde qu‘il a inventé, en vue de découvrir en lui de nouvelles idées. »
Les diversités linguistiques et culturelles, l’écart de départ peuvent s’avérer très féconds, chacun prenant conscience, au contact des autres, de ses propres postulats implicites et pouvant ainsi les critiquer.
L’écart
Il y a peut-être entre Jany (et Stella Baruk) et moi un écart de départ. Par exemple, il parle de cours moyen première année. À ce niveau, dont je n’ai pas l’expérience, il est peut-être utile de faire des leçons (peut-être...). Mais la réponse au problème qu’ils posent peut se situer en amont de leurs classes, c’est-à-dire au cours préparatoire et au cours élémentaire.
Quand il écrit, par exemple, qu’il « me parait vain, superficiel et trop ambitieux d’aborder les changements d’unité d’aire tant que la notion de surface n’est pas suffisamment maîtrisée » on peut se demander qui décide d’aborder ? Et si ce sont les enfants dans leur course olympique ? En fait, ils ne décident pas, ils se trouvent soudainement plongés dedans.
La connaissance commence avec le problème qui est une réalité objective. Un problème, c’est d’abord une surprise. Une attente est déçue. Les événements ne prennent pas l’allure que l’on prévoyait. Il faut faire face.
Avec la MN, il ne s’agit plus de maîtriser des programmes imposés à coups d’ingurgitation de situations-types, mais de développer ses aptitudes à élaborer des stratégies (ce qui est de plus en plus nécessaire dans ce monde qui s’ouvre).
Je ne pense pas qu’il y ait de programmation sûre et définitive à établir. Elle s’établira « naturellement » quand on laissera les enfants construire leur mathématique, en s’appuyant légèrement sur le savoir descendant du maître. » (Pomès)
Mais même dans nos groupes de méthode naturelle, beaucoup d’enseignants n’osent encore y croire totalement. Ils ont raison. Il ne faut pas se lâcher les mains avant d’avoir assuré ses pieds. En art enfantin, cela a été la même chose. On a commencé à y croire seulement quand des collègues ont pu faire l’expérience à fond. Mais là, c’était plus facile parce que ni parents, ni administration n’en avaient souci.
Certains enseignants se soucient tellement du savoir du maître qu’ils ne pensent pas à le faire descendre à la rencontre du savoir montant des enfants. L’administration, les politiques, les spécialistes, les agrégés pensent également à élever le niveau des enseignants. Pour transmettre (distribuer ?) des connaissances. Mais ils se trompent sur l’emplacement du moteur. Nous, nous insistons sur la dynamique de la méthodologie, sur l’unité méthodologique du mode d’acquisition des connaissances (celle de la science). Leur altitude dissimule peut-être une crainte de perte de pouvoir.
Attitude
Devant l’erreur de Nathalie, Jany Gibert va lui demander ainsi qu’à la classe – pour que Nathalie et le groupe en constatent la nécessité – de modifier la représentation. En cette circonstance, c’est lui qui est le maître d’œuvre, c’est lui qui tient les ficelles, c’est lui qui sait où il veut les mener. Au CM1, j’aurais peut-être agi de la même façon. Et au CP-CE, il m’a fallu beaucoup de temps pour changer d’attitude.
Mais Jany et moi, nous pouvons nous raccorder sur l’utilité de l’erreur.
« Une théorie riche, même si elle court beaucoup de risques d’être réfutée peut, même dans son échec, nous fournir encore des informations. »
« Une théorie réfutée garde souvent une certaine valeur comme approximation. »
J’aime aussi quand il écrit :
« D’une manière générale, nous travaillons beaucoup sur nos erreurs. Nous réfléchissons collectivement pour les critiquer et pour tenter de comprendre le pourquoi et le comment de ces erreurs (erreurs de structure, de représentations, de démarches). »
Alors, nous allons pouvoir dans notre communauté de praticiens fonctionner suivant le tétragramme poppérien.
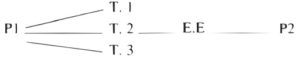
P = problème T = théorie EE = Élimination de l’Erreur.
Ainsi, en passant par T. 1 = traditionnel – T. 2 = calcul vivant – T. 3 = recherches libres – T. 4 = méthode naturelle, nous allons aller de P1 = problème de l’enseignement des mathématiques à P2 = conquête de la connaissance par l’enfant (acquisitions, oui, mais surtout élan, dynamisme, démocratie).
Et par l’élimination des erreurs, on débouchera sur un problème de meilleure qualité. Et nous irons peut-être aussi sur le chemin d’une « épistémologie sans sujet » centrée sur l’affirmation de l’autonomie de la connaissance objective par rapport au sujet qui la produit. Connaissance objective signifiant connaissance communicable et intersubjectivement valable.
Paul Le Bohec, le 14 juillet 1990, La Mézière
Article paru dans le Nouvel Éducateur document n°228, recherches et pratiques en mathématiques, supplément au Nouvel Éducateur n°31 de septembre 1991, p.8-10
N. B. : Toutes les citations non signées sont tirées du livre de Renée Bouveresse, Karl Popper, Éditions J. Vrin, 1978.