La trace (2)

Dans la première partie de cette étude, parue sous le titre de La Trace dans L’Éducateur n° 18-19 du 15 mai-1er juin 1965, Le Bohec montre comment l’activité libre de l’enfant, et même le dessin libre, débouchent sur la géométrie. Voici donc la suite de cet exposé.

Le point
Voyez comme dans toutes les classes, les enfants passent par ce stade du pointillé. C’est surtout un procédé de décoration et d’enrichissement. Parfois, cela va jusqu’à la submersion complète, et le dessin, trop chargé, coule. Mais il faut bien faire cette expérience pour connaître les limites du pointillé ; cela suffit à préserver les flottes futures. Et puis, on a parfois l’âme torpilleuse et il faut quelquefois achever à la mitrailleuse ce que l’on a construit. Vous voyez, les enfants ne négligent pas cette dimension ponctueuse du pinceau et s’en régalent longuement.

La ligne
Qu’est-ce que la ligne ? C’est un point qui se déplace (la bille du bic, la pointe du pinceau). Ou encore c’est, mathé­matiquement parlant, un objet à une seule dimension. En réalité, les enfants n’en sont pas à ce stade et leur ligne a une épaisseur. Mais dans leur esprit, ils voient l’avenir ; ils savent bien qu’ils n’en sont encore qu’au début de la cure d’amaigrissement. Il faut permettre le tâtonnement sur toute la ligne en offrant les traceurs nécessaires, mais aussi de vastes supports (tableaux verticaux ou horizontaux) qui permettent le geste ample et détendu. Il est aussi certainement possible d’in­venter des machines à lignes pour une étude expérimentale objective. Personnellement, j’en tiens déjà une : c’est une sorte de génératrice à cycloïdes, épicycloïdes et sinusoïdes qui, à partir d’une lettre matrice : O, I, V, Δ, permet à un crayon d’engendrer des effets inattendus. Le point du crayon bille se déplace lentement et rythmiquement, dans le O par exemple. Mais le support se déplace et il naît de cette conjugaison des mouvements une épicycloïde. Ce qui est bien, c’est que cette abstraction sera reversée dans la vie par l’enfant qui examinera par exemple la trajectoire de la valve de son vélo – ou la plume d’un baromètre enregistreur.

La surface
C’est une ligne qui a pris de l’ampleur ; c’est-à-dire que la longueur n’y écrase plus la largeur. C’est parfois aussi une ligne qui se mord la queue et fait une partition de l’espace. Naturellement, il nous faut également favoriser le tâton­nement des surfaces. Là, qu’avons-nous à offrir ?
Il y a bien sûr, une fois de plus, la peinture. Et l’on a vu que certains enfants ne tâtonnent que dans une direction purement géométrique.
Mais, il existe certainement d’autres techniques. Sont-elles toutes bonnes, indifféremment ? Je ne le crois pas.

À ce sujet, je me suis longtemps posé la question de savoir pourquoi je rejetais certains jeux sensoriels à base de carrés, de triangles et de losanges de couleurs. Je les trouvais artificiels. Et, pourtant, j’aurais pu appliquer ce vocable à quelques-unes des machines dont je pensais grand bien. Et je crois que j’ai trouvé une réponse. Une machine, une technique a le droit d’être aussi artificielle qu’elle le veut, pourvu qu’un courant puisse aller de la vie jusqu’à elle et d’elle jusqu’à la vie. El dans le cas de ces jeux sensoriels, c’est vrai, le courant ne passe pas. Et au lieu de susciter la recherche, ils provoquent l’ennui.

Pour ce tâtonnement, la mosaïque m’a paru idéale parce qu’elle obligeait vrai­ment à sentir la surface. Un jour, j’avais voulu aider des camarades carre­leurs qui réalisaient une mosaïque de hasard dans un garage. Mais je n’avan­çais pas parce que je n’avais vraiment pas le sens de la surface. Ce sens me paraît important et mérite qu’on lui consacre du temps.

Mes tentatives de mosaïques dans ma classe se sont soldées par un échec : la matière première que je pouvais mettre à la disposition des enfants était trop rare et trop précieuse pour per­mettre un tâtonnement foncier. Or, il ne faut jamais perdre ça de vue : pour qu’un tâtonnement conduise à une maîtrise, il faut une débauche d’expé­riences. Ah ! si j’avais eu un four ! Mais, j’ai trouvé un ersatz assez satis­faisant : les collages. Ici, je semble quitter le monde de la trace. Mais, en y réfléchissant bien on constatera que, avant de planter son ciseau dans le vif du papier, l’enfant a tracé, au moins virtuellement, une ligne qu’il s’efforce de suivre.

Évidemment, sur le plan artistique, je n’obtiens pas ce que d’autres obtiennent. Mais sur le plan surfaces, c’est bon. Si on ne donne à l’enfant que du simple papier de couleur uni, cela fera un exercice pauvre. Avec des pages de revues, la malice et la fantaisie de l’enfant peuvent se donner libre cours : des choses amusantes ou profondes apparaissent. Et il en redemande.

Sur les conseils de Freinet, je vais maintenant parler de ma machine à géométrie dans l’espace. (Ici, il ne s’agit pas à proprement parler de traces mais de lignes matérialisées dans l’es­pace.)

C’est un cube construit avec des cornières de meccano. Sur la face infé­rieure et sur la face supérieure, j’ai fixé une plaque carrée d’isorel perforé. On peut joindre chaque trou du haut à chaque trou du bas par le moyen d’une ficelle munie à chaque extrémité d’un élastique. C’est une bonne machine puisqu’elle plaît aux enfants qui y vont un peu comme ils vont à l’Ariel. La création de chaque enfant est soumise à la critique de la classe et l’auteur rectifie s’il en éprouve le besoin. On dit aussi ce que l’on re­marque ; et les notions de plans, plans parallèles, intersections, plans perpendiculaires sont déjà assimilées, avec des retours à la vie : le cirque, la tente d’indien, le paravent, etc. On peut tâtonner aussi sur les pyramides en mettant un crochet en haut ou en bas, ou plusieurs crochets... On peut aussi coudre une ficelle et les créations obtenues sont très riches. Et puis, ce n’est pas abstrait puisqu’il s’agit d’isorel, de ficelles, d’élastiques. Et les découvertes sont reversées dans la vie.

« Oh ! monsieur, j’ai remarqué que les poteaux du préau étaient dans le même plan... »

J’ai donc examiné quelques idées d’ou­tils existant ou à créer pour le tâtonnement géométrique.
Mais, dans ce domaine, l’école moderne a encore autre chose à offrir. Car ce qui précède peut paraître farfelu, utopique, irréel, importun et trop bousculant.
Prenons donc la bonne géométrie clas­sique, la rassurante euclidienne qui nous est, à tous, plus ou moins familière et qui nous a laissé de si bons souvenirs. Avons-nous quelque chose à offrir, là ? Oui : notre conception de l’enseignement à base de recherches et de créa­tions, ou pour mieux dire, la pédagogie de l’invention et de la découverte mise au point par Delbasty-Bernardin, Jessé, etc.

Voici, par exemple, la relation de recherches faites dans la classe de Méheust de Pleunieur-Bodou (CM-FEP). Incidemment, il avait été ques­tion de bissectrice.

« Oh ! oui, on sait ce que c’est : la bissec­trice partage un angle en deux parties égales.
- Moi, j’ai un bon truc pour tracer les bissectrices. Sur un côté de l’angle, j’élève une perpendiculaire n’importe où et je prends le milieu du troisième côté du triangle formé. Il n’y a plus qu’à joindre.
– Pas possible ! Mais est ce que c’est juste ?

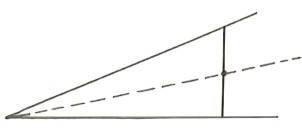
– Eh ! bien mesurons au rapporteur.
– Ah ! non, les deux angles ne sont pas égaux.
– Moi j’ai une autre idée. Il n’y a qu’à pencher le troisième côté.

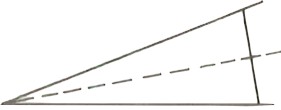
– Vérifions. C’est plus vrai. »
Mais le maître, tatillon, discute l’égalité des angles.
« Comment faire pour le pencher juste, ce troisième côté. »
Soudain un garçon s’écrie :
« J’ai trouvé ! À partir de l’angle, je construis un losange, j’en efface la moitié et je prends le milieu du troisième côté. »

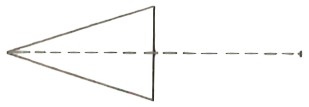
Cette fois-ci c’est juste. Mais le maître, insupportable, dit :
« Oui, parce que vous aviez un double-décimètre. Mais si vous n’aviez eu qu’un compas ? »

Nouvelles recherches dans le bonheur de l’invention et de la critique de la découverte...
Et puis voici que le rectangle se pré­sente sur le tapis. On relève le défi. Ah ! ce qu’il en pose de problèmes, ce rectangle ! Et on en trouve des solutions ! Plus originales les unes que les autres. Et l’un des enfants, amou­reux de la bissectrice qu’il a conquise, réussit à la fourrer partout et à faire avancer la classe entière. Un autre fait son miel de la perpendiculaire...

... Puis vient le problème des diagonales.
« Que se passe-t-il lorsque l’angle formé par les diagonales varie ? »

On essaie sur les figures et on commence à voir quelque chose. Mais un garçon construit deux diagonales en bois creu­sées aux extrémités pour qu’une ficelle puisse y coulisser.

Et les expériences recommencent.
Le jeudi suivant, Méheust m’en parle : « Tu vois, on aurait pu étudier à quel moment il faut lâcher de la ficelle, à quel moment elle est la plus courte, etc. »
Aussitôt, j’éprouve le besoin de ramener ma science.

« Mais, ça ne doit pas varier.
– Et pourtant ça varie.
– Oui, parce que la construction est mal faite : la pointe n’est pas au milieu des deux diagonales.
– Ah ! tu crois. Tu m’étonnes pourtant.
– Mais, écoute : tu as a²+b² = c², or, c² est constant, donc a²+ b² est constant.
– Peut-être, mais je ne suis pas convaincu.
– Quelle tête de mule ! Le lieu géomé­trique des points dont la somme des distances aux extrémités d’un segment est constante est un cercle.
– Tu sais, je ne suis pas fort en géométrie. Ça doit être vrai puisque tu le dis, mais ça m’étonne. »

Je   reviens   chez   moi   et j’explique l’affaire à Hervé. Il est d’abord de mon avis si pleinement mathématique, si conforme aux idées reçues, puis de l’avis de Méheust, puis il ne sait plus. « Pourtant ça me parait clair. »
Et soudain, je me souviens :

« Quel idiot ! Ce lieu géométrique dont je parlais, c’est l’ovale que le jardinier trace avec une ficelle attachée à deux piquets. »

Alors, nous recherchons ensemble la source de mon erreur et nous nous apercevons que de a²+b² = constante on ne peut pas du tout inférer que a+b = constante. Ouais, j’ai bonne mine.

Si j’ai relaté cette discussion, c’est pour montrer :

– que l’on ne peut pas se fier à des idées qui étaient parfois mal reçues ;
– que le refus de Méheust de se plier à des raisonnements qui n’emportaient pas son adhésion a été efficace ;
– que la critique nous a fait progresser et ouvert de nouveaux horizons ;
– que cette expérience me fait réflé­chir : on ne m’y reprendra plus. Cependant, Méheust et Hervé s’en souviendront également parce que dans notre recherche, il s’est mêlé de l’affectif, de l’humain.

Ceci rejoint le propos de André Revuz qui dit qu’on ne doit jamais accepter aveuglement les idées de l’auteur du livre mais qu’on doit les expérimenter et les discuter : ce n’est qu’à ce prix que l’on comprend les maths.

À propos de géométrie, Méheust a un peu continué ses expériences et il m’a avoué éprouver le vertige devant le monde qui pourrait s’offrir à nous. (Heureusement, il y a un correcteur de vertige : la préparation au certificat. Ce certif, on l’a encore devant soi pour quelques bonnes années, des années de sécurité. Un bravo pour les esprits modernes qui lui permettent de sur­vivre. Et l’on ne comprend vraiment pas pourquoi Jaurès n’en voulait déjà plus en 1888.)

Mais, on peut aller encore plus loin dans cette recherche de la pédagogie des mathématiques. Delbasty y est allé et personnellement j’aimerais bien pouvoir l’y suivre. J’ai hâte de voir publiées ses recherches sur « le petit rectangle » qu’il est en train de mettre au point. Car nous travaillons encore trop lourdement avec nos grosses pattes. Il faudrait savoir discerner les petits chemins des mathématiques. À vrai dire, avant Delbasty, quelqu’un s’est-il interrogé sur la sensibilité des enfants aux figures et aux espaces ? Ah ! que nous avons encore besoin d’écouter, de sentir, de nous faire toute réception ! Alors, attendons la publica­tion des travaux de Delbasty.

Mais je ne vais pas terminer ainsi. D’ailleurs, la géométrie, n’est-ce pas infini comme l’espace ? Et, puisque j’ai commencé à l’assommer, je voudrais bien l’achever complètement, le vieil homme géométrique. Vous savez que je fais également des recherches pédagogiques de gymnastique dans la nouvelle optique de « tous les départs avant 8 ans ». Et là j’en ai découvert des géométries. Je ne donne ici que des indications qui devraient permettre des départs d’expérience.

Ma classe est très grande (80 m²) et entre les tables et le tableau il y a un grand espace rectangulaire où chaque enfant, tout à tour créateur et exécu­tant, peut inventer des évolutions. Tout d’abord, mes 7-8 ans ont inventé des croisements. Mais comme ils se faisaient au centre du rectangle ça n’a pas marché. Alors, il a fallu introduire des retards (de départs, de vitesses, de distances) qui ont rendu possibles les croisements. D’autres évolutions ont également été créées. Par hasard, je me suis mis à dessiner ce qu’ils faisaient sur le tableau (c’était une abstraction). Et voici que Pierrot qui est fils de « plantrier » (puisque son père, métreur, fait des plans) a lui aussi dessiné des gymnastiques à base de triangles, de losanges, de cercles. Et nous les avons réalisées dans la cour. Et puis, pendant un certain temps, l’habitude de dessiner l’évolution avant l’exécution s’est installée dans la classe. Chaque déplacement était ainsi programmé par une flèche de couleur. Et l’exécution était surveillée et criti­quée par le reste de la classe.

N’est-ce pas merveilleux cette réalisa­tion d’une idée abstraite et cette géo­métrie qui rentre par les jambes ?

Et quelles portes s’ouvrent sur l’avenir ! À un niveau plus élevé, il pourrait y avoir ces allers et retours de l’idée à la réalisation. Une idée pourrait être réalisée pratiquement ce qui obligerait à en retravailler l’expression géométri­que puis on effectuerait un nouveau passage au banc d’essai et ainsi de suite jusqu’à raffinement. Et cela sur des paroles, des chants, des musiques. Ne faut-il pas aussi lancer les tâtonnements sur le plan de la mise en scène, de la chorégraphie ?

Enfant du peuple, à ça aussi, tu as droit. Tu ne seras peut-être pas metteur en scène ou chorégraphe, mais ce monde là te sera aussi ouvert parce que tu en auras eu à temps les clés.

Géométries... Géométries...

Paul Le Bohec

Article paru dans l’éducateur n°1, la part du maître, 1^er octobre 1965, p.7-12