J’ai animé récemment deux séances de méthode naturelle de maths (M.N.M.) dans un CE2. Il m’est apparu clairement que :
- On doit partir de créations libres. C’est à dire qu’elles peuvent aussi bien se fonder sur le réel que sur l’imaginaire. Ou sur un mélange des deux. Il faut que le groupe puisse accepter chaque création sans émettre de jugement. Chaque enfant doit être accepté dans sa démarche personnelle.
- Plus que n’importe quelle autre pratique pédagogique – et ça, ça m’a vigoureusement étonné – la M.N.M. est un outil étonnant d’investigation et d’appropriation du monde. En y réfléchissant, je pense qu’elle se focalise un temps sur le « moment de la structure ». Et ce moment est capital au niveau de la construction du savoir. Mais il ne faut pas oublier que ce n’est qu’un moment dans un aller-retour constant entre la vie complexe et profuse de la structuration. C’est d’ailleurs ce qui fait la validité de la M.N.M. En une heure, on s’était lancé sur la piste des stabiles de Calder, des abribus, de l’architecture, des logos, de la sculpture. Mais ça ne touchait pas que les nombres et les lignes mais, aussi, la linguistique, les anagrammes, les relations entre les mots etc. Tout ça en une heure –et j’en oublie – Imaginez une année scolaire, une scolarité !
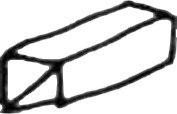
- Pour prendre ma part du maître « introducteur et agrandisseur de liberté », j’ai tracé au hasard, en fermant les yeux quatre lignes sur un papier. J’ai appelé ça : « le développement à plat d’une chose inconnue ». J’ai plié suivant les traits et avec un peu de scotch, j’ai fait un volume. Comme c’était biscornu, j’ai dit : « C’est une statue. » Et je l’ai posé sur l’armoire. Et ça pouvait déboucher sur les stabiles de Calder. Mais Nathan, lui, a pensé à un abribus. Et il a dessiné le développement suivant :
![]()
Il a été surpris du résultat. Mais la classe lui a emboîté le pas, et pendant quinze jours, elle s’est vautrée dans la fabrication de volumes réguliers. Daniel et moi, on aurait pu s’en agacer.
Mais je lui ai parlé de la dialectique : « Quand on va vers une saturation, en même temps se construit une frustration. » Et c’est à toi de guetter le premier pas de côté qui va se produire dans la série des créations. Il suffira que tu soulignes l’apparition de cette nouvelle chose. Et si le groupe est près de la saturation, il basculera. Ou bien ce ne sera que le demi-groupe. Ou qu’un seul enfant qui suivait les autres pour faire comme tout le monde mais qui s’aperçoit soudain que le nouveau domaine lui convient parfaitement.
- La part du maître est parfois difficile à prendre – mais il ne faut jamais s’en culpabiliser, sinon, c’est foutu -. Moi, j’ai voulu agrandir le champ des libertés alors que Sabrina avait spontanément fait « un développement de cube » avec des rectangles ! On ne regarde pas assez. Mais on n’entend pas non plus assez. Pour l’abribus de Nathan, je ne me suis pas arrêté à la réflexion d’un garçon qui avait dit : « Il n’y a qu’à en faire deux. » Et son idée n’a pas été exploitée parce que je ne l’ai pas soulignée.
« Naturellement » on loupe plein de choses. Mais ça n’a pas d’importance si l’on fait suffisamment confiance à la puissance cognitive du groupe qui est beaucoup plus riche d’idées, plus clairvoyant, plus intelligent que le pauvre maître bloqué dans ses routines de pensée et ses inquiétudes.
Et Monique l’a montré dans le dernier bulletin maths de 88 : « Alors là, je suis stupéfaite, je n’ai rien osé dire, je n’ai pas osé leur dire que le mois précédent, je leur avais fait construire la table de Pythagore et qu’on l’avait construite de cette façon-là. Ils l’avaient faite. Ils m’avaient écoutée poliment. Mais ça leur était passé par-dessus la tête. Maintenant ils savent parce que ce sont eux qui l’ont redécouverte. »
Je crois que l’on pourra souvent le constater (Et on a encore tellement de choses à découvrir !) : ce n’est que lorsqu’il s’agit de leur(s) affaire(s) à eux – et non de celle du maître – que cela se fixe.
« Connaître, c’est primairement computer, c’est à dire opérer sur des signes-symboles-formes par le moyen de signes-symboles-formes. » (Edgar Morin)
C’est pour cela que par minitel on va être assez vite limités. Tiens : « Le minitel est limité. »
Ça fait penser à Victor Hugo « Les souffles de la nuit... »
Comme quoi, il suffit toujours de partir.
Paul Le Bohec, 7-11-88
Texte paru dans le bulletin Naturellement math N°1, Janvier 1989, p.17-18