Compte rendu de la séance de la commission CP du département 35.
La classe est un SE-CP-CE1 de 14 élèves.
Au tableau, une dizaine de créations recueillies sur les carnets et transcrites la veille après la classe. Nous n’en verrons étudier que quelques-unes.
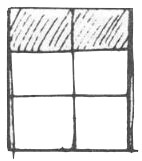
– Ce dessin donne des notions de paires et de pairs. On aurait pu se diriger vers la combinatoire : combien de façons de noircir deux cases sur six ? La maîtresse avait cette piste là en tête. Mais tout a tourné autour du rectangle. Elle l’a facilement accepté. Elle renonce facilement à ses projets pour se fixer sur l’intérêt des enfants.
– C’est un quadrilatère. Pourtant le nom n’a été donné qu’une fois mais il est retenu. Sans doute parce que c’est un drôle de nom de bête.
– Les côtés sont pareils. Comment le savoir ? Une fillette « mesure » en mettant des points assez régulièrement espacés et elle compte. Mais la maîtresse, impossible, refait la même chose en séparant irrégulièrement les points. Une autre fillette pose successivement mais irrégulièrement le bout de son index. Enfin, on arrive à la ficelle. Les spectateurs allaient s’ennuyer tellement c’était connu pour eux. Mais il y avait Élodie qui n’avait pas encore saisi la mesure et tâtonnait originalement. Pourtant on avait vu ça plusieurs fois. Mais elle n’était pas encore mûre. Il fallait lui laisser faire sa démarche : elle mettait l’extrémité de la ficelle sur son doigt et la posait irrégulièrement en comptant. Cependant, la solution donnée par un garçon (CE1) mit une lumière future au bout de l’un de ses tunnels. Un jour elle comprendra que c’est vers cette lumière, au bout de ce tunnel, qu’il vaudrait mieux qu’elle regarde.
![]()
– Naturellement on parle du 2 et du 5 absents. Il est fait référence à une trouvaille précédente sur 1-3-5-7 dont le présent travail est une extension. Puis on propose de continuer 9-10-12-13. Xavier complète par un 0 avant le 1 : 0-1 3-4 6-7 9-10 12-13.
Élodie saute la série sur le plancher : 0-1 je saute, 3-4 je saute. C’est de la mathématique dansée. On aurait pu penser à la valse...
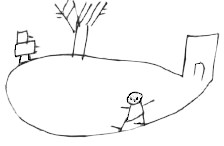
- Que faire de ce dessin ? On aurait pu laisser les enfants partir sur l’histoire d’un cosmonaute. Mais nous sommes en mathématique. On voit le déplacement. Les personnages circulent à gauche de l’allée : latéralité ou code de la route. Référence à un pêcheur qui pêchait de la gauche, côté jardin, ce qui le mettait côté cour quand il faisait demi-tour.
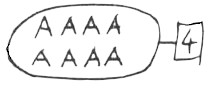
– C’est pas 4, c’est 8. Non, c’est 4, en liant par deux verticalement : on a 4 paires (père de chaussons, mère de chaussons). On aurait pu lier horizontalement. On pourrait faire des sous-ensembles en écrivant 8 = 4 + 4 = 2 + 2 + 2 + 2 + 2.
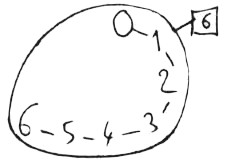
– Pourquoi l’étiquette 6 ? – Parce qu’il y a six nombres. – Ah ! oui ? – Oui... non c’est 7. – Le 0 aussi est un nombre. - Ah ! oui !
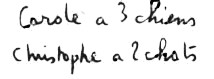
– La maîtresse a en tête le problème d’hier avec 4 et 2 qu’on égalisa par 4 - 1 et 2 + 1. Et elle voudrait taquiner les enfants sur l’égalisation impossible. Mais les enfants s’évadent vers 3 + 2 = 4 + 1= 5 + 0 = 5. La maîtresse rentre sa taquinerie. Elle la réserve pour plus tard.

– On pourrait arriver à 2 - 1 = 1.
C’est un bref aperçu, mais les carnets sont pleins de créations.
– Moi, jamais je n’y arriverai : je suis surprise de tout ce que vous voyez là-dedans. Moi je ne vois rien.
– Mais tu n’es pas seule, il y a les enfants. C’est vrai qu’il y a un problème de sécurisation du maître dans un certain savoir. Il faut être formé. On pourrait facilement se co-former.
– Ce n’est pas difficile, ce sont souvent les mêmes choses qui reviennent, ça vient vite.
– Moi, nulle en maths, après trois ans de panique et d’agrippement désespéré à la bouée du livre, je commence, cette année, à voir des situations mathématiques. Beaucoup basées sur la numération parce que je vois à peu près clair là-dedans. Mais pas seulement et ça, ça me réjouit. Cette année, j’ai osé essayer un peu pour commencer, comme ça, une fois, pour voir. Et depuis je ne me suis pas arrêtée.
Mais pour me sécuriser et pour obtenir des répits de silence, je leur ai donné les cahiers auto-correctifs de la C.E.L. Et je m’aperçois qu’ils réussissent bien leurs opérations alors qu’on n’en a pas fait. Comme dit une mère d’élève avec étonnement : c’est drôle, ils savent sans avoir appris.
Paulette – Moi aussi, je me sécurise un peu par rapport à l’inspection et aux parents. Le soir, dans 001, je cherche des situations qui correspondent à ce qu’on a inventé et examiné et je les polycopie comme exercice.
Certaines fois, j’arrive en classe avec du travail préparé. C’est rare, mais quand ça arrive, je suis bien contente : j’ai bonne conscience, je suis sérieuse. Eh ! bien, le soir, je ne sais pas pourquoi, je suis fâchée après moi, je m’en veux.
– Mais oui, le matin, tu as une bonne conscience de rendement traditionnel (acquisition et toute la merde : passivité, obéissance, reproduction, renoncement, mort). Et, le soir, tu n’as pas une bonne conscience Freinet : il n’y a pas eu de créations, d’échanges, de critiques, de recherches d’hypothèses, de tâtonnements, de liens affectifs et de liant affectif et d’acquisitions supérieures. Et tu as contraint le char à rester dans les ornières de tes préoccupations.
Paulette – C’est vrai. Mais il y a quelque chose de plus : nous savons où nous en sommes avec les enfants. Mais quand je travaille traditionnellement, je suis comme les autres : je sème mon bon grain, sans trop savoir où il lève et quand il lève.
– Oh ! moi, j’ai fait le pas. J’ai abandonné toute référence au livre depuis longtemps. La classe est suffisamment nourrie par ses créations et on travaille avec intensité.
– C’est vrai, je pourrais le faire maintenant car je m’aperçois que les enfants assimilent beaucoup. Et puis il y a des retours en arrière, des reprises qui constituent des révisions et qui permettent à d’autres de prendre leur essor à leur tour quand ils se trouvent mûrs. L’an prochain, je me lancerai.
– Comment as-tu commencé ?
– Par des observations sur la constitution des groupes : CP, 4 filles avec des noms en boucle et un garçon : Xavier ; CE, 4 garçons et 1 fille.
Et puis j’ai regardé les griffonnages sur les cahiers. Et j’ai donné des carnets.
– À mon avis, il faut faire une différence entre ce qu’on pourrait appeler mathématique vivante par l’extension du calcul vivant à diverses situations nées de la vie ou proposées par le maître. Et la mathématique créative entièrement basée sur les créations, sur l’expression des enfants (ce qui n’empêche pas les nombreuses références à la vie). Aujourd’hui, par exemple la latéralisation, le code de la route, la mesure, le rythme (la valse), les chiens, etc.
On a toujours fait ça à l’école moderne :
![]()
Mais il faudrait plutôt faire ça :
![]()
C’est, je crois, l’opinion actuelle de Lèmery, les enfants sont sous-alimentés en abstraction.
Mais en vérité, ne serait-ce pas plutôt :
![]()
Et même mieux :
![]()
en ajoutant le palier du jeu au niveau abstrait, le jeu mathématique.
– Moi je pose la situation au tableau seulement quand je sais par avance ce que je vais pouvoir en tirer.
– Eh ! bien, tu te prives de l’apport des enfants. Ils sont souvent plus riches, plus inventifs qu’on ne le croit. Tu devrais leur faire plus confiance. Et puis c’est presque toujours à côté de ce qu’on a prévu qu’on apprend le mieux.
– Bon j’essaierai le samedi pour commencer.
– Bien sûr, tu verras que les enfants ont des choses à dire qui te surprendront peut-être. Même si tu ne peux pas toujours répondre, ça ne fait rien. Il faut apprendre à ne pas rester toujours dans les sécurités de son savoir. C’est un entraînement, c’est une formation que tu te donneras peu à peu avec l’aide des camarades.
– Moi, lorsqu’une situation se présente, on l’étudie oralement. Et quelquefois on va au tableau.
– Oui mais c’est là toute la différence. Tu ne bases pas les maths sur la création mais sur l’occasion. Tu ne crées pas mille occasions, tu attends le bon vouloir d’une seule. Il te manque la créativité mathématique qui est plus riche que l’étude et la perception des structures à connaître. Et puis la mathématique c’est très peu oral, c’est à base de symboles écrits ou dessinés.
– Moi, je suis étonnée de ce que tu peux faire avec les enfants. Tu acceptes tout sans crainte. Tu es capable de le faire.
Paulette – Mais je me suis formée dans le groupe en méthode naturelle de formation des maîtres. Et je ne fais pas de complexe : si je ne trouve rien, les enfants trouveront. Et si on ne trouve pas, on verra à faire mieux quand ça reviendra.
– Mais toi, tu ne t’es pas formée lors des réunions dont parle Paulette. Tu ne créais pas et ce n’est vraiment que sur ses créations que l’on assimile le plus et le plus vite.
– Moi, j’ai travaillé un moment en mathématique créatrice. Mais sous l’impulsion du second groupe de maths (à partir de situations proposées), j’étais repartie vers davantage de recherche de structures. C’est intéressant. Mais je comprends bien que comme ceci, on débouche sur autant de structures. Et c’est plus vivant, plus riche, plus global. L’enfant n’est pas déporté de ses chemins, il peut se construire et c’est le groupe d’enfants qui le déphase juste ce qu’il faut. Et non le maître. Il y a plus d’autonomie. Il y a un tâtonnement individuel. Je vais peut-être m’y remettre.
– Une chose étonnante, c’est ce qui se passe chez moi avec Pascal (CE1) qui est un non matheux total. Il n’est pas dans le coup, mais il s’y met bizarrement. Il dit de curieuses choses. Par exemple :
– Il y a une boîte à œufs. Combien il y en a ?
Nathalie, fille d’épicière dit : – 6 ou 12.
– Mais non c’est une boîte inventée.
– C’est pair ou impair.
– Qu’est-ce que c’est ça pair ou impair ? (Alors qu’on ne fait que ça depuis un mois !)
Il dit :
– C’est pair. Et c’est juste avant 21. Alors c’est 19 ?
– Mais non c’est pair.
– C’est 20 ?
– Oui c’est ça.
Et brusquement on s’aperçoit que Pascal a compris les nombres pairs. Un déclic s’est produit. Avec lui c’est presque toujours comme cela ; il faut que ça passe par une création personnelle tordue.
– Et toi, Paulette, es-tu contente de t’être lancée dans cette aventure de mathématique créative ?
– Ce n’est pas une telle aventure. Il faut que je vous dise : il y a deux ou trois ans, j’avais décidé d’être sérieuse et de me préoccuper d’acquisitions. J’ai fait ce qu’il fallait. Mais les enfants et moi, nous nous sommes ennuyés comme jamais. Et les acquisitions, je ne suis pas sûre qu’elles étaient fixées non plus. Il y manquait trop le liant affectif.
Tandis que maintenant, je suis sûre que ça va marcher. Ça marche déjà. Quand on fait une leçon sur les acquisitions comme habituellement, on croit que c’est compris. Mais les chemins de la fixation sont bien plus compliqués que cela. Il y a l’élan, la camaraderie, les hypothèses que la maîtresse laisse détruire quand elle ne donne pas le coup de pouce. Bref, il y a les critiques successives et l’impossibilité d’échapper à la réalité, au vrai ou faux. Et c’est ainsi qu’on maîtrise et qu’on comprend.
Mais je vais vous dire une autre chose. Quand je les vois tous là assis devant le tableau, même les petits de 3, 4, 5 ans et qu’ils regardent et qu’ils écoutent et qu’ils participent tous, ça me fait quelque chose. On ne sait pas trop comment ils s’y prennent, ils grappillent sans doute, les choses circulent en eux on ne sait comment, c’est émouvant. Et chaque jour, ils amènent leur chaise et ils s’assoient avec les autres devant les créations du tableau. Et chaque jour ils viennent. Et chaque jour, ils restent jusqu’au bout !!!
Paul Le Bohec
Texte paru dans l’éducateur n°12, 20 avril 1976, p.7-9
Séance de la commission CP 35 (P. Forget, R. Bigot, A. Le Charpentier, O. Jegou, M. Jannin, E. Perrigault, D. et Y. Agaësse, C. Le Garrec-Odile, J. et P. Le Bohec, J.-C. Sanson).


