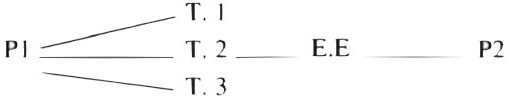Il faut réfléchir à ce à quoi nous sommes sur le point d’aboutir sur le plan de l’enseignement des mathématiques. Nous savons que la pédagogie Freinet exige le contact avec la vie. Et elle l’a réalisé en créant le calcul vivant. Mais il s’agit maintenant de créer la mathématique vivante.
Pour voir clair, pour faire le point de la situation, voyons un peu les choses dans leur mouvement. Quelle a été la démarche des pédagogues du calcul ? Ils sont passés de l’emploi des petits cailloux, aux marrons du boulier, aux perles du boulier (plus abstrait), aux doigts de la main pris par unités, aux doigts des deux mains pris par ensemble (ou parties d’ensemble), aux jetons groupés en constellation, puis au Cuisenaire constitué d’ensembles coloriés où les unités sont indistinctes. Et le prochain pas à franchir, n’est-ce pas tout simplement l’absence de tout matériel spécialisé ? Il faut comprendre les raisons qui ont motivé l’abandon successif des diverses techniques d’enseignement.
Dans son livre La Genèse du nombre chez l’enfant, Piaget montre qu’il y a d’une part des séries de quantité inégales ordonnées : 1 < 2 < 3 < 4 < 5 < 6 < 7 < 8 ...
et d’autre part des classes de quantités égales, par exemple : 3 carottes, 3 choux, 3 navets, 3 poissons, appartiennent à la même classe 3.
Il dit que le nombre apparaît lorsque l’on fait la multiplication logique de la série par la classe.
La série ne suffit pas, ni la classe.
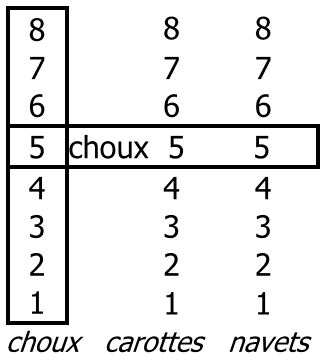
5 choux se trouve dans la série verticale entre le 4 choux et le 6 choux.
Mais, il se trouve aussi dans la classe horizontale des 5. Le comptage unité par unité ne donne que l’ordre, la place de la collection dans la série. Il faut aussi que l’on sache quel est l’attribut de la classe à laquelle appartiennent les collections : 5 choux, 5 carottes, 5 navets, c’est le cardinal 5. Donc le nombre est à la croisée de l’ordinal avec le cardinal. C’est le produit de la multiplication logique.
Or, le comptage par unité du matériel petits cailloux ne concernait que l’ordre. C’est pour cette raison qu’un pas fut franchi lorsqu’on groupa les petits cailloux (ou les jetons par constellation). Dans le Cuisenaire, la notion d’ensemble est encore plus importante. C’est vers elle que l’on a progressé. Et c’est pour cette raison que partant du calcul où le comptage importe surtout, on en arrive à la mathématique où l’on porte l’accent sur les structures. On passe de l’objet individuel à l’objet dans le groupe. Comme on a fait un progrès considérable à l’École Moderne en considérant l’enfant dans son individualité propre et dans son appartenance au groupe (individualisation de l’enseignement et pédagogie de groupe).
Lorsqu’on prend conscience de la double nature de l’homme : individu et être social, on peut en tirer des conséquences pratiques.
De même, il y a le double aspect du calcul et de la mathématique. Je l’ai constaté dans ma classe : ils sont inséparables. J’avais décidé de porter l’accent sur la mathématique : tant pis pour le calcul, je n’y penserai que plus tard.
Et je suis déjà rassuré parce qu’on a fait aussi du calcul. Alors, je crois que l’on peut mettre l’accent sur la formation du mathématicien en lui offrant l’occasion de prendre conscience des différents modes de relations qui existent entre les choses.
Il est peut-être préférable de ne pas être trop pressé et de moins rechercher les résultats spectaculaires, en prenant soin d’observer, tout simplement, la vie.
Il suffit d’ouvrir l’œil et le bon, c’est-à-dire l’œil structural.
Je viens de lire le tâtonnement expérimental de Freinet. Il distingue :
1) Les pionniers, c’est-à-dire ceux qui déjà solidement armés et munis d’une soif inextinguible affrontent l’inconnu qu’ils explorent par tâtonnement expérimental.
2) Ceux qui suivent leurs traces et refont le même chemin mais dans d’autres conditions.
On nous jette toujours dans les jambes qu’il est ridicule de croire que les enfants auront à refaire toutes les expériences de l’humanité.
Et peut-être que si justement. Peut-être pas toutes les expériences, mais beaucoup d’expériences. Mais dans des conditions totalement différentes.
En effet, l’humanité n’a progressé lentement que parce qu’il a fallu une quantité considérable de hasards pour que des lois de la nature puissent être saisies. Tout était à faire, on ne pouvait se référer à rien. On ne pouvait transposer ce qui avait été trouvé dans d’autres domaines parce que rien n’avait été trouvé. On n’était pas armé sur le plan conceptuel. On ne s’était pas forgé les outils du raisonnement. Rien n’avait été transmis (ou très peu) parce qu’avant il n’y avait rien. Tout le monde était pionnier. Tout le monde tâtonnait sans même savoir qu’il y avait quelque chose à trouver sans avoir la faim de cette chose.
Est-ce que l’on pensait à penser ? Et les formes de pensée les plus primitives, les plus aberrantes, qui pouvait dire qu’elles étaient néfastes, puisque l’expérience n’avait jamais été faite ? Le critère de la justesse d’une idée, c’est la pratique, mais à quoi se réduisait la pratique ? À rien pour ainsi dire. Dans ces conditions, comment la marche en avant n’aurait-elle pas été d’une extrême, extrême lenteur ? Tandis qu’aujourd’hui, même en supposant que l’enfant doive faire toutes les expériences de l’humanité, il les ferait à une vitesse considérable. Il n’y aurait plus ces temps morts interminables, ces temps figés, ces temps gelés qui ne se dégelaient que par moments sous l’impulsion de circonstances dues aux hasards, à des hasards rares.
Car, quel est l’élément qui peut faire progresser un chercheur ? C’est la critique. Maintenant, presque toujours, pour l’enfant, quelqu’un sait et il peut apporter sa critique. L’enfant sait que les choses, les idées, les lois existent autour de lui, il peut en avoir faim. Il peut avoir un élan vers la connaissance et se mettre en marche par ce qu’il voit de la vie. Or, en éducation, la solution semble être de développer par tous les moyens la critique (bien entendu la critique objective qui aide, qui respecte le chercheur, qui respecte sa marche en avant, qui ne tue pas sa faim, mais l’excite).
Mais on sait bien maintenant que, pour savoir, il faut redécouvrir. C’est en forgeant... C’est en créant des structures qu’on maîtrise les structures, c’est en créant des symboles qu’on maîtrise la symbolisation (la sienne et celle des autres).
Mais si l’enfant crée seul, sans témoin, il sera l’homme seul des premiers âges. Heureusement la critique peut venir de ses pairs. Pourquoi les savants cherchent-ils en équipe ? Parce que, seuls, ils ne suffisent pas pour assumer la fonction critique à un niveau suffisant : il faut toute une équipe. Et si les pairs ne jouent pas le rôle, alors il faut que le maître sache, lui, afin qu’il puisse désembourber le char quand il le faut. Oh ! Pas tout de suite, quand le groupe a déjà longuement tâtonné. Mais, il faut puisque nous en sommes au début de la marche en avant, que l’enfant, que le groupe réussisse ; que par des victoires successives, il acquière un élan irrésistible et définitif.
Oui, le maître doit savoir. Pour aider les enfants à accéder au deuxième étage, au troisième, pour les aider à rejoindre l’équipe des pionniers (être pionnier il n’y a que cela qui vaille la peine pour l’être humain), il faut que le maître ait déjà fait le chemin. Et, dans ce domaine nouveau de la mathématique, nous sommes en retard, incontestablement. Nous n’avons pas encore fait le chemin. Et parfois nous serions tentés de nous donner les beaux gants du dédain des mathématiques. D’un manque, d’une insuffisance, nous aimerions faire une supériorité. Oui... enfin... peut-être... Mais alors nous serions d’un autre âge.
Heureusement, à l’École Moderne, nous ne sommes pas seuls. S’il y a le tâtonnement de l’individu, il y a aussi le tâtonnement du groupe. Et, chez nous, il y a déjà des pionniers qui ont fait le chemin et qui peuvent aider -et s’aider- de leurs critiques tous ceux qui veulent suivre le chemin.
Nous avons des revues, des bulletins, des périodiques, des mensuels, des cahiers de roulement. Nous avons, à notre disposition, la critique de nos pairs et si cela ne suffit pas, la critique des maîtres ès mathématiques qui sont prêts à nous aider, parce que nous aider, c’est les aider à avoir des élèves mieux formés, ayant encore des faims et un élan.
Alors qu’est-ce qu’on attend ?
Paul Le Bohec
Texte paru dans l’éducateur N°15-16-17, 1er-15 mai-1erjuin 1966, mathématiques modernes, p.5-8.