Qu’est-ce que le sens mathématique ?
À Vence, Madeleine Porquet me disait que des savants belges ont dit aux institutrices de leur pays : « Avec les petits, soyez très prudentes. Faites bien attention. »
Oui, nous sommes d'accord, nous sentons bien que les jeunes êtres qui arrivent dans nos petites classes sont très fragiles et c'est une grande crainte pour l’éducateur, de briser définitivement quelque ressort secret et précieux.
Oh ! oui, prendre garde mais à quoi ? Et comment ? Hélas, cela nous reste à découvrir.
Depuis les journées de Vence, je ne suis plus si tranquille, je croyais avoir trouvé mais je m’aperçois que je suis encore en deçà.
L’expression « mathématiques sans les nombres » m’a surpris et je me suis aperçu par exemple que, dans la vie, nous évaluons sans cesse. Le conducteur à son volant évalue sans arrêt des vitesses, des largeurs, des degrés de résistance de la chaussée, des directions, des probabilités de maladresses, des courbes, des inclinaisons, des marges de sécurité, tout cela sans formuler de nombres.
Et le goal qui apprécie des trajectoires, des hauteurs, des épaisseurs, des angles, des vitesses de joueurs, de vent, de ballon. Et le chasseur !
Cette forme des mathématiques remplit notre vie : c’est l’expérience et une certaine forme d’intelligence (perméabilité à l’expérience) qui confèrent l’excellence dans ce domaine.
Peut-on s’en préoccuper à l'école ? Je ne sais ?
Dans ce domaine, il suffit peut-être de vivre.
Pour le reste, je propose un planning assez complet que j'ai en grande partie expérimenté l'an dernier et que je vais utiliser plus à fond cette année. II se divise en deux parties.
D'une part le paravent à l'abri duquel on se livrera au travail profond. Mais il ne faudrait pas que l'existence du paravent empêchât le travail en profondeur par sa lourdeur matérielle qui pourrait étouffer, écraser, détruire.
(1) petite fiche portant le détail des 10 marches du brevet
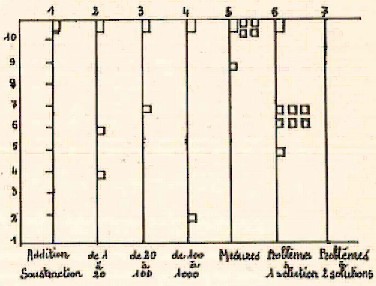
Paravent des brevets obligatoires
1- Une colonne pour les additions-soustractions. C’est le fichier A découpé en 10 tranches.
2- Une colonne pour les nombres de 1 à 20 avec des pièces de monnaie.
10 : écriture des nombres de 1 à 20
9 : de 15 à 20 10 5 2 2
8 : de 10 à 20 pièces de 1 2 5
7 : de 1 à 15 pièces de 10 2 2 1
6 : de 1 à 15 pièces de 1
5 : de 1 à 10 mélange 5 2 2 1
4 : de 1 à 10 pièces de 2
3 : de 1 à 10 pièces de 1
2 : de 1 à 5 avec 2 F 2 F l F
1 : de 1 à 5 avec pièces de 1 F
0
3- Nombres de 20 à 100 avec pièces de monnaie de 50 20 20 10 5 2 2 1
4- Nombres de 100 à 1000, même procédé
L’utilisation des pièces de monnaie pour la numérotation est intéressante parce qu’elle s’inscrit dans la vie, dans la classe et hors de la classe.
5- Mesures (après expérimentation libre)
10 : estimer une minute, une contenance
9 : estimer une longueur, un poids
8 : avant 1 heure - 2 h moins 25 etc
7 : après 1 heure – 2 h 10, 3 h 15, 4 h 25
6 : verser 57 cl, 65, 78, avec les 1 2 5 10 20 cl
5 : calculs de capacités
4 : tracer des lignes, couper des ficelles à la demande
3 : mesurer des longueurs, table, tableau, murs
2 : 5 objets poids indiqué, poser d’abord les poids marqués
1 : peser 5 objets, poids inconnu
6- Problèmes à 1 solution
Problèmes nés de la vie collective de la classe (calendrier, colis, etc.) ou problèmes vrais présentés par des camarades. Ex : Nous avions 156 F. Nous achetons un carnet 26 F. Il reste ?
Le signe seul est important. Le point est acquis même si le résultat est incorrect.
7- Problèmes à 2 solutions
Lorsqu’un enfant a ses deux brevets de résolution écrite, on peut être tranquille sur son compte et il peut travailler à d’autres brevets sans que le maître ait quoi que ce soit à craindre.
Ces brevets de contrôle s’étalent généralement sur l‘année entière. C’est en quelque sorte le plan de travail annuel qui se trouve affiché en permanence et qui se lit d’un coup d’œil. II pourrait être compris comme la systématisation, le passage au stade du réflexe inconditionné de ce qui a été librement exploré l’année précédente.
Cette mécanisation devrait être davantage étalée dans le temps. Par exemple on pourrait porter la division au CM et la multiplication au CE2.
C’est une revendication qui n’est pas sans importance. On se préoccupe trop à l’école primaire de l’acquisition des mécanismes qui obscurcit l’horizon au point de masquer l’acquisition du sens mathématique qui à l’époque des règles et machines à calculer est de plus en plus l’essentiel.
Pour cela il faut non seulement séparer les mécanismes mais relâcher leur emprise en étalant les acquisitions sur de plus longues années avec révisions constantes et entretien de la forme opérationnelle.
(À suivre)
Paul Le Bohec
Article paru dans l’éducateur n°4, 15 novembre 1960, p.129-130
(Suite des pages 5 et 6 de l’éducateur n°3 du 1er novembre 1960)
