Avant de poursuivre, il faut que je revienne un peu en arrière, car j’ai oublié un point important.
On a vu qu’après diverses corrections, on peut accéder au palier de la première réussite. Et lui succède aussitôt la série des répétitions pour la vérification et pour l’intégration. Mais, ce qui facilite le mieux l’intégration, c’est la construction d’un système de repères.
Repères
Oui, j’ai réussi une fois. Mais c’est peut-être par hasard. Comment vais-je me mettre en situation de pouvoir toujours recommencer ? Et il me faut trouver, en outre, un moyen d’économiser du temps. Car je suis pressé de redevenir disponible pour d’autres recherches, pour de nouvelles intégrations qui seront pour moi autant d’armes, autant d’outils pour affronter la vie ou pour augmenter les possibilités de jouissances que j’en pourrais tirer.
Pour cela, il faut que je passe du stade de la « présence » nécessaire, de la réflexion consciente au stade de la disponibilité, du réflexe automatique.
Un exemple
Nous venons de recevoir une gazinière mixte neuve. Pour le gaz il y a deux commandes : une pour le grand brûleur du fond, une pour le petit brûleur de devant. Pendant un certain temps, nous réussissons l’allumage en présentant successivement l’allumette aux deux brûleurs, en ouvrant brièvement, s’il le faut, celui qui ne convient pas.
Mais ce tâtonnement peu élégant m’énerve assez rapidement. Alors je me construis une référence. Je me dis : le petit brûleur, c’est la manette de gauche. Or ma main gauche est inférieure à ma main droite. Donc pour allumer le brûleur inférieur, je tourne la manette du côté de ma main inférieure.
J’associe donc, par ce procédé, la taille du brûleur et la place de la commande. Et, à partir de là, je ne me trompe plus jamais, je réussis à tous les coups. Si bien que ça devient automatique. Je ne sais pas ce que devient alors ma référence. Est-ce que, inconsciemment, je me la répète encore, de plus en plus rapidement. Ou bien les actes ne se succèdent-ils pas automatiquement, dans une chaîne de stimuli-réponses ? Je ne puis le savoir puisque c’est devenu inconscient. Et je ne m’en préoccupe pas, sinon, où serait l’économie ?
Par la suite, je découvrirai qu’à côté de chaque manette, il y avait un schéma de référence.
Pour retenir les numéros de téléphone, j’ai des repères arithmétiques : Roger c’est 3 et 3 = 6, 3 et 6 = 9 → 33.63.69. Yves c’est 35 (I et V) + 15 + 15 → 35.50.65.
Dès que j’entends un numéro, ça se met à fonctionner automatiquement dans ma cervelle : je construis des associations entre les éléments et je m’en souviens.
Autres systèmes de repères : les cartes routières, les marques des sauteurs en longueur, les plans, les procédés mnémotechniques.
Spécificité des repères
Si vous réfléchissez un peu, vous constaterez que vous aussi, vous avez vos systèmes de repères. Mais chacun peut avoir ses systèmes particuliers.
Pour bien préciser cette idée, je prends l’exemple particulièrement intéressant d’un couple d’amis. Je n’hésite pas à le faire parce que c’est à partir de la vie quotidienne que nous devons construire notre savoir.
Quand ils voyagent, Lucette ne voit que les bouquets d’arbres, les groupes de maisons, les bords des rivières, les parcs, les mares, les toits, les murs. Mais il suffit qu’elle passe une seule fois dans un endroit pour s’en souvenir définitivement. Et cela aide Georges, le conducteur, qui a parfois besoin d’une confirmation de la validité du chemin poursuivi.
Mais Georges ne voit rien de ce qu’elle voit, non seulement parce qu’il est occupé à conduire mais parce que ce n’est pas dans sa nature. Lucette se baigne dans les paysages successifs. Georges voit des parallèles, des symétries, des similitudes, des complémentations. À l’étape, il se régale de l’étude des cartes. Il en est vraiment amoureux. Et il se fabrique parfois des itinéraires « économiques » qui se révèlent désastreux dans la réalité parce qu’ils sont pleins de bosses et de virages.
Il faut dire qu’il est fils de cheminot roulant. Et citadin par surcroît. Et il a passé son enfance dans les horaires et l’entrelacs des rues. Chez lui, le train de six heures et demie, c’était le rapide 525 de 18 h 32. Et le jardin produisait des patates et des fleurs de haricots et de petits pois qui donnaient des gousses. Il vivait dans un monde quadrillé.
Lucette, par contre, avait vécu une enfance de campagne libre et de bord de mer et rêvait ses voyages. Et un jardin, c’était rempli de coccinelles, de chenilles rayées, de papillons, de véroniques azurées et de mouron tango.
On sent à quel point on peut être conditionné par son ancien style de vie.
Mais, il y a une autre source de structuration du monde. Car, chez eux, il y a un bizarre renversement. Lucette qui ne sait jamais où elle se trouve au cours d’un voyage, localise parfaitement le moindre bruit dans sa maison. Et à n’importe quel moment du jour et de la nuit elle peut deviner l’heure à cinq minutes près. Et quand on lui raconte une anecdote ou un fait de vie, elle demande toujours des précisions sur le lieu et le moment car elle a l’impression, sans cela, qu’elle ne pourra pas comprendre.
Mais Georges, dans sa maison, ne sait jamais où ça se passe. Et là nuit, c’est à huit heures près qu’il sait l’heure. C’est peut-être une question de sécurité personnelle. Il est certain que de nombreux êtres ont besoin d’un quadrillage serré du temps et de l’espace pour se repérer et se sentir vivre.
Donc, on le voit par ces exemples, on peut être vraiment différent de nature et de conditionnements.
La mathématique personnelle
Et ceci nous conduit à une réflexion sérieuse. En effet, il faut qu’on sache bien que si l’enfant a pu survivre de 0 à 6 ans, c’est qu’il a pu se construire des quantités de repères de tous ordres. Mais si on lui impose ex abrupto et autoritairement un système tout fait, efficace et technocratique, on risque de briser quelque chose en lui.
Chacun devrait pouvoir partir de ses constructions personnelles. Et il faudrait qu’il puisse communiquer « sa » mathématique. C’est quand on explique qu’on comprend : la seule exposition de ses idées susciterait des remises en ordre, des restructurations.
S’il avait accès à la mathématique des autres, chacun pourrait bénéficier de la critique des exemples et il pourrait choisir d’abandonner ou non ses repères, ses procédés personnels.
Mais il ne faudrait pas que l’école induise l’idée qu’il y a une mathématique supérieure à l’autre, la mathématique économiquement rentable. Car certains êtres produisent de la poésie, de la rêverie. Et, de cela, le monde a aussi besoin. Si tout le monde fonctionnait de la même façon, quel ennui ce serait, où serait l’enrichissement par la différence ?
Donc, dans l’idéal, il faut aider chacun à construire sur des bases personnelles, non seulement « sa » mathématique, mais « son » football, « sa » musique, toutes ses techniques de survie et de jouissances. Quelquefois, il y a de longues maturations dont la rentabilité est provisoirement nulle et qui débouchent finalement sur des processus étonnants auxquels on n’avait pu penser jusque-là. Parce qu’on était obsédé de rentabilité à court terme ou parce qu’on nous avait obligés à nous en obséder.
Mais il est temps de donner un exemple :
Danièle Agaësse qui pratique la création mathématique à longueur d’année a étudié les « textes mathématiques » d’un enfant de CE2 (Pascal). En voici un :
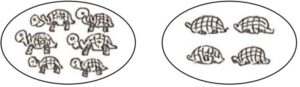
« Nicolas achète une ou deux tortues. Mais que choisit-elle ? Une salade ou deux ? Laquelle ? »
Les autres enfants proposent successivement toutes sortes de solutions, celle-ci et celle-là. Mais Pascal répond toujours non. À la fin, ses camarades lui demandent la réponse. Il en désigne deux.
– Mais comment veux-tu qu’on découvre lesquelles c’était puisque tu ne nous as donné aucune indication.
– Oui, mais moi, je savais.
Et ce genre de textes dure un long moment. Mais, dans l’ambiance chercheuse de la classe, les textes de Pascal se nourrissent d’un peu plus de mathématique.
Au bout d’un certain temps, pour le sonder, Danièle lui propose de dessiner des cases et d’y placer des nombres. Il le fait, en décalant des suites de nombres.
– Tu vois, toi aussi, tu es capable de faire des textes de ce genre. Je vais le porter au tableau pour qu’on l’étudie collectivement.
Mais Pascal proteste avec vigueur :
– Ah ! non, ça ce n’est pas ma mathématique !
Et sa mathématique à lui, c’est plein de devinettes (pouvoir de celui qui les propose et qui domine par le pouvoir de son savoir. Pascal est un aîné : il a des compensations de pouvoir à réaliser.) C’est aussi rempli de problèmes de maisons, de petit escargot sur le dos de sa mère, de chemins pour aller à la maison, de villes, de planètes...
Ce qui est curieux c’est que ses textes sont souvent choisis par la classe pour une étude plus approfondie. Ils posent problèmes. Et pas que mathématiques. Et il y a naturellement écho chez les camarades qui sont séduits par l’ailleurs, par l’affectivité sous-jacente ou par la difficulté de découvrir de la mathématique là-dedans.
Et il y en a nécessairement car l’enfant a besoin d’exprimer l’état de ses relations dans la famille. Et la représentation de relations, c’est de la mathématique.
Et en restant résolument lui-même, sans concession ni destruction de sa personnalité, Pascal apporte beaucoup à la classe. Son incertaine présence au monde, qui est peut-être un défaut pour lui, devient une qualité dans le groupe de recherche. Et la reconnaissance de son apport l’aide à devenir un peu plus présent au monde.
La classe aussi doit pouvoir construire d’abord sa mathématique à partir de ce qu’elle est, sur sa personnalité. On ne devrait songer à provoquer des ouvertures, par la correspondance par exemple, qu’à partir du CM. Jusque-là, on a de quoi se nourrir.
Limites
Mais attention, là encore il y a des limites à droite et à gauche. À gauche, si on se sent vraiment responsable, il faut penser à donner des armes de survie aux enfants : latéralisation, aisance corporelle, vision rapide, compréhension des situations. Il faut les aider à se constituer des repères. Sinon, on continuera de rencontrer des bambins roulant à vélo, à gauche, dans les virages pentus d’une route nationale. On ne peut trop rêver dans ce monde.
Cette importante digression étant achevée, nous pouvons reprendre ensemble la construction de notre grille de lecture du tâtonnement expérimental.
15. Extension du champ d’application de la loi
(du truc, de la recette, de la solution, de la découverte)
Variation des conditions d’application
Bon, j’ai trouvé une solution très acceptable. Pour la neige poudreuse tout au moins. Mais, attention, quand elle est verglacée, ça change. Et quand c’est de la soupe, c’est encore autre chose. Et puis, surtout, quand on sort des rails sécurisants, quand on est sur de la neige vierge de toute trace, c’est une autre paire de skis qu’on a aux pieds : ils rêvent de leur indépendance.
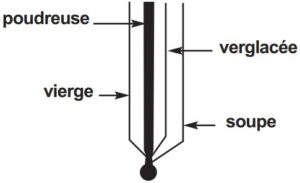
Peu à peu, la maîtrise s’étend à tous les terrains.
Nota. – Sur les schémas suivants, l’épaississement du trait traduira à la fois l’extension de la maîtrise et la densité de l’intégration de la nouvelle technique à l’être.
Isolement des composantes internes et approfondissement (spécialisation)
Lorsque la maîtrise s’installe un peu plus, on devient disponible. Et on s’aperçoit qu’à l’intérieur du ski de fond il y a de nombreux éléments différents. Et on peut progressivement se fixer sur l’un ou l’autre pour y développer son plaisir.
On peut s’apercevoir par exemple que ce qui plaît c’est :
– La descente : alors on pourra s’orienter sérieusement vers le ski alpin. Tout ne sera pas à recommencer, certains acquis subsisteront. Mais il faudra adapter.
– Le décollage : on peut s’orienter vers le saut de ski. On retrouvera les « rails » et les skis, mais on perdra les bâtons.
– Les virages et la liberté que procure la possibilité de faire varier volontairement sa trajectoire. Ça peut conduire au slalom.
– La promenade : alors on peut faire des randonnées tranquilles. Mais là-dessus peut se greffer l’idée de :
– La mesure : si on aime se mesurer à soi, on peut faire de grands parcours quotidiens (la 10 + la 15) ou de grandes randonnées. Ceci pour éprouver ses possibilités, pour s’approcher de ses limites, pour savoir où elles se placent.
Et si on a besoin de se mesurer aux autres (besoin naturel ou provoqué), c’est la compétition qui conviendra tout spécialement : ski alpin : descente, slalom spécial, slalom géant ; ski de fond ; saut à ski... On abandonne alors l’activité globale pour se spécialiser.
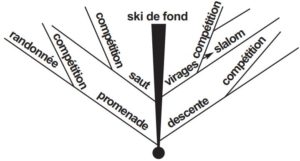
On voit à quoi peut mener l’acquisition d’une technique : d’abord à un élargissement du champ de la maîtrise, puis à une exploitation approfondie de ses paramètres qui peut aller jusqu’à une spécialisation.
Il serait intéressant d’appliquer ce qui précède à tous les apprentissages. Et de repérer les techniques de base à acquérir. Il semble par exemple que le ski de descente soit un dérivé du ski de fond et non l’inverse. Par lequel commencer ?
Mais chaque acquisition apporte encore beaucoup plus.
(à suivre)
Paul Le Bohec
Texte paru dans l’éducateur n°10, 10 mars 1978, p.35-36
(Suite des articles parus dans les n°4, 5, 7 et 8 de l’Éducateur, année 1977-78)